분할 정복 알고리즘

저번 포스팅에 이어서 알고리즘 문제 해결 책의 새로운 챕터를 맞이하여, 문제를 풀기 전에 정리되어 있는 분할 정복의 도입 부분과 예제 풀이 부분 등에 대해 정리해보도록 하자.

책에서는 C++를 이용해서 코딩하지만, 스터디를 위해 사용하기로 한 언어가 JAVA이기 때문에 코드는 JAVA로 작성되었으며, 책의 내용을 나름대로 재구성하여 작성하였다.

먼저, 분할 정복이란 무엇인지 알아보자.

분할 정복(Divide & Conquer)은 가장 유명한 알고리즘 디자인 패러다임으로 쉽게 말해 각개 격파라고 할 수 있다. 각개 전투? 예비군.. 하..? 갑자기..? 아무튼, 분할 정복 패러다임을 차용한 알고리즘들은 주어진 문제를 둘 이상의 부분 문제로 나눈 뒤 각 문제에 대한 답을 재귀 호출을 이용해 계산하고, 각 부분 문제의 답으로부터 전체 문제의 답을 계산해 낸다.

분할 정복을 사용하는 알고리즘은 크게 세 가지의 구성 요소를 갖게 된다.

문제를 더 작은 문제로 분할하는 과정(Divide)
각 문제에 대해 구한 답을 원래 문제에 대한 답으로 병합하는 과정(Merge)
더이상 답을 분할하지 않고 곧장 풀 수 있는 매우 작은 문제(Base case)

분할 정복을 적용해 문제를 해결하기 위해서는 문제에 몇 가지 특성이 성립해야 한다. 문제를 둘 이상의 부분 문제로 나누는 자연스러운 방법이 있어야 하며, 부분 문제의 답을 조합해 원래 문제의 답을 계산하는 효율적인 방법이 있어야 한다.

분할 정복은 많은 경우 같은 작업을 더 빠르게 처리해 준다. 그렇다면, 어떤 경우 사용할 수 있는지 알아보자.

수열의 빠른 합.

//1부터 n까지의 합을 계산하는 반복 메소드.(단, n >= 1)
//1부터 n까지의 합을 반환한다.
int sum(int n){
  int ret = 0;
  for(int i = 1; i <= n; ++i){
    ret += i;
  }
  return ret;
}

//1부터 n까지의 합을 계산하는 재귀 메소드.(단, n >= 1)
//1부터 n까지의 합을 반환한다.
int recursiveSum(int n){
  if(n == 1) return 1;
  return n + recursiveSum(n-1);
}

위의 sum과 recursiveSum 메소드는 1부터 n까지의 합을 구하는 방법을 일반적인 반복문과 재귀 호출을 통해 구현한 메소드이다. 위와 똑같은 일을 하는 분할 정복을 적용한 fastSum이라는 메소드를 작성할 수 있다.

먼저, 1부터 n까지의 합을 n개의 조각으로 나눈 뒤, 이들을 반으로 잘라 \({n \over 2}\)개의 조각들로 만들어진 부분 문제 두 개를 만든다. (우선, n은 짝수라고 가정한다.)

\[fastSum() = 1 + 2 + ... + n = (1 + 2 + ... + {n \over 2}) + (({n \over 2} + 1) + ... + n)\]

첫 번째 부분 문제는 fastSum(\({n \over 2}\))로 나타낼 수 있지만, 두 번째 부분 문제는 그렇지 않다. 문제를 재귀적으로 풀기 위해서는 각 부분 문제를 1부터 n까지의 합 형태로 표현할 수 있어야 하는데, 위의 분할에서 두 번째 조각은 a부터 b까지의 합 형태를 가지고 있기 때문이다. 따라서 다음과 같이 두 번째 부분 문제를 fastSum(x)를 포함하는 식으로 바꿔 써야 한다.

\[({n \over 2} +1 )+ ... + n = ({n \over 2} + 1) + ({n \over 2} + 2) + ... + ({n \over 2} + {n \over 2}))\]

\[={n \over 2} \cdot {n \over 2} + (1 + 2 + 3 + ... + {n\over 2})\] \[={n \over 2} \cdot {n \over 2} + fastSum({n \over 2})\]

\[({n \over 2} + 1) + ... + n = ({n \over 2} + 1) + ({n \over 2} + 2) + ... + ({n \over 2} + {n \over 2})\]

\[= {n \over 2} \cdot {n \over 2} + (1 + 2 + 3 + ... + {n \over 2})\] \[= {n \over 2} \cdot {n \over 2}\]

공통된 항 \({n \over 2}\)을 따로 빼내면 \(fastSum({n \over 2})\)형태로 나타낼 수 있다. 따라서 다음과 같이 쓸 수 있다. \(fastSum(n) = 2 \cdot fastSum({n \over 2}) + {n^2 \over 4}\) (n이 짝수일 때)

이러한 아이디어를 실제 구현하면 아래와 같은 코드로 나타낼 수 있다. 위의 분한은 짝수인 n에 대해서밖에 동작하지 않기 때문에, 홀수인 입력이 주어질 때는 짝수인 n-1까지의 합을 재귀 호출로 계산하고 n을 더해 답을 구하게 된다.

//짝수 조건: n은 자연수
//1 + 2 + ... + n을 반환한다.
int fastSum(int n){
  if(n == 1) return 1;
  if(n % 2 == 1) return fastSum(n-1) + n;
  return 2*fastSum(n/2) + (n/2)*(n/2);
}

시간 복잡도 분석.

fastSum과 recursiveSum 두 메소드 모두 내부에 반복문이 없기 때문에, 두 메소드가 종료하는 데 걸리는 시간은 순전히 메소드가 호출되는 횟 수에 비례하게 된다. recursiveSum의 경우 n번의 메소드 호출이 필요하다. 반면 fastSum은 호출될 때마다 최소한 두 번에 한 번 꼴로 n이 절반으로 줄어들게 된다. 오! 때문에 fastSum의 호출 횟수가 훨씬 적으리란 것을 예상할 수 있다.

다음은 fastSum(11)을 실행할 때 재귀 호출의 입력이 어떻게 변화는지를 이진수로 표현한 예이다.

fastSum(1011₂) = fastSum(1010₂) + 11
fastSum(1010₂) = fastSum(101₂) x 2 + 25
fastSum(101₂) = fastSum(100₂) + 5
fastSum(100₂) = fastSum(10₂) x 2 + 4
fastSum(10₂) = fastSum(1₂) x 2 + 1
fastSum(1₂) = 1

재귀 호출을 할 때 n의 이진수 표현의 마지막 자리가 1이면 0으로 바꾸고, 마지막 자리가 0이면 끝자리가 없어진다는 것을 알 수 있다. 따라서 fastSum의 총 호출 횟수는 n의 이진수 표현의 자릿수 + 첫 자리를 제외하고 나타나는 1의 개수가 된다. 두 값의 상한은 모두 lgn이므로 이 알고리즘의 실행시간은 O(lgn)이 된다.

행렬의 빠른 제곱.

n x n 크기의 행렬 A가 주어질 때, A의 거듭제곱(power) \(A^m\)은 A를 연속해서 m번 곱한 것이다. 이것을 계산하는 알고리즘 자체는 어려울 것이 없지만, m이 매우 클 때 A를 구하는 것은 꽤나 시간이 오래 걸리는 작업이 된다. 행렬의 곱셈에는 일반적으로 O(\(n^2\))의 시간이 들기 때문에 곧이곧대로 m - 1번의 곱셈을 통해 \(A^m\)을 구하려면 모두 O(\(n^2 * m\))의 연산이 필요하다. 절레절레… 하지만 분할 정복을 이용하는 눈 깜짝할 새에 연산이 가능하다.

\(A^m = A^{n \over 2} \cdot A^{n \over 2}\) 앞서 사용한 방법을 똑같이 이용하면 \(A^m\)를 구하는데 필요한 m개의 조각을 반으로 나눌 수 있다.
```
//정방행렬(행과 열이 같은 행렬)을 표현하는 SquareMatrix 클래스가 있다고 가정한다.
class SquareMatrix;
//n*n 크기의 항등행렬(중심 대각선은 1, 나머지는 0인 행렬)을 반환하는 메소드
SquareMatrix identity(int n);
//A^m을 반환한다.
SquareMatrix pow(final SquareMatrix A, int m){
//기저 사례 A^0 = 1
if(m == 0) return identity(A.size());
if(m % 2 > 0) return Math.pow(A, m - 1) * A;
SquareMatrix half = Math.pow(A, m / 2);
//A^m = (A^(n/2) * A^(n/2))
return half * half;
}
```
시간 복잡도 분석.

m이 홀수일 때, \(A^m = A \cdot A^{m-1}\) 로 나누지 않고, 좀더 절반에 가깝게 나눈게 좋지 않을까 생각을 할 수 있다. 예를 들어 \(A^7\)을 \(A \cdot A^6\)으로 나누는 것이 아니라 \(A \cdot A^3 \cdot A^4\)로 나누는 것이 더 좋지 않은가 하는 것이다. 실제로 문제의 크기가 매번 절반에 가깝게 줄어들면 기저 사례에 도달하기까지 걸리는 분할의 횟수가 줄어들기 때문에 대부분의 분할 정복 알고리즘은 가능한 한 절반에 가깝게 문제를 나누고자 한다.

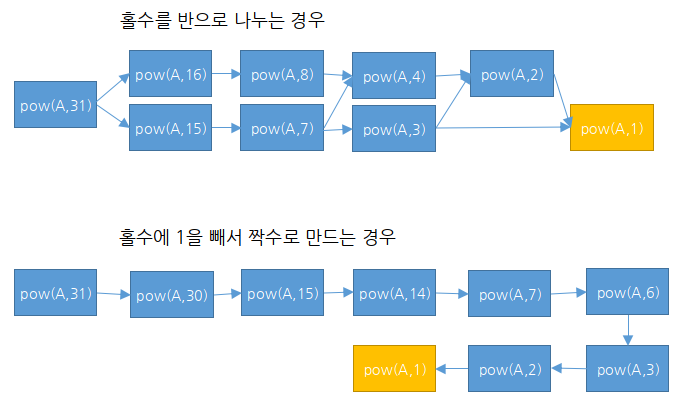행렬의 거듭제곱을 위한 두 가지 분할 방식의 비교 위 사진은, 두 가지 분할 방식을 이용해 pow(A, 31)을 계산할 때 필요한 부분 문제 간의 의존 관계도를 나타낸다. pow(A, x)를 계산하는 과정에서 pow(A, y)를 호출해야 한다면 두 값은 화살표로 연결되어 있다.

첫 번째 방법에서 pow(A, 8)은 pow(A, 15)를 계산할 때도 호출되고 pow(A, 16)을 계산할 때도 호출되므로, 모두 두 번 호출된다는 것을 알 수 있다. 따라서 pow(A, 8)과 pow(A, 7)을 계산할 때 사용하는 pow(A, 4)는 모두 세 번 호출된다.

이와 같이 같은 값을 중복으로 계산하는 일이 많기 때문에, m이 증가함에 따라 pow(A, m)을 계산하는데 필요한 pow 메소드의 호출 횟수는 m에 대해 선형적으로 증가하게 된다.

이것은 같은 문제라도 어떻게 분할하느냐에 따라 시간 복잡도 차이가 커진다는 것을 보여주는 좋은 예이다. 절반으로 나누는 알고리즘이 큰 효율 저하를 불러오는 이유는 바로 여러 번 중복되어 계산되면서 시간을 소모하는 부분 문제들이 있기 때문이다. 이런 속성을 부분 문제가 중복된다고 부르며, 동적 계획법이 고안된 계기가 된다.

카라츠바의 빠른 곱셈 알고리즘

병합 정렬이나 퀵 정렬도 이러한 분한 정복 알고리즘을 적용한 수열의 정렬 알고리즘이며, 여러 병합 과정을 가진 분할 정복 알고리즘 중의 한 예가 카라츠바(러시아 수학자 이름)의 빠른 곱셈 알고리즘이다. 두 개의 정수를 곱하는 알고리즘으로 수백 자리, 수만 자리는 되는 큰 숫자들을 다룰 때 주로 사용한다. 이러한 큰 숫자들은 컬렉션(혹은 배열)을 이용해 저장해야 한다. 아래의 코드는 두 자연수의 십진수 표기가 배열에 주어진다고 할 때, 이 둘을 곱한 결과를 계산하는 가장 기본적인 방법을 표현한 것이다.

//두 큰 수를 곱하는 O(n^2)시간 알고리즘
void nomarlize(List<Integer> num){
  num.add(0);
  //자릿수 올림을 처리한다.
  for(int i = 0; i < num.size(); ++i){
    if(num.get(i) < 0){
    int borrow = (abs(num.get(i)) + 9) / 10;
    num.set(i+1, num-borrow);
    num.set(i, num + (borrow * 10));
    }
    else{
      num.set(i+1, num.get(i) / 10);
      num.set(i, num % 10);
    }
  }
while((num.size() > 1) && (num.get(num.size() - 1) == 0)){
  num.remove(num.size() - 1);
}
}
//두 자연수의 곱을 반환한다.
//각 List 컬렉션에는 각 수의 자릿수가 1의 자리에서부터 채워진다.

이 List 컬렉션들은 곱한 수의 각 자릿수를 맨 아래 자리부터 저장하고 있다. 이렇게 순서를 뒤집으면 입출력할 떄는 불편하지만, A.get(i)에 주어진 자릿수의 크기를 \(10^i\)로 쉽게 구할 수 있다는 장점이 있다. 따라서 A.get(i)와 B.get(j)를 곱한 결과를 C.get(i+j)에 저장하는 등, 훨씬 직관적인 코드를 작성할 수 있다.

또 하나 눈여겨볼 점은 자릿수 올림을 처리하는 nomarlize에서 자릿수가 음수인 경우도 처리하고 있는 것이다. multiply에서는 덧셈밖에 하지 않기 때문에, 자릿수가 음수가 될 일이 없다.

//예: multiply([3, 2, 11, 16, 15, 4]) = 123 * 456 = 56088 = [8, 8, 0, 6, 5]
List<Integer>multiply(final List<Integer> a, final List<Integer> b){
  List<Integer> c = new ArrayList<>();
  for(int i = 0; i < a.size() + b.size() + 1; ++i){
    c.add(0);
  }
  for(int i = 0; i < a.size(); ++i){
    for(int j = 0; j < b.size(); ++j){
      c.set(i+j, a.get(i) * b.get(j));
    }
    nomarlize(c);
  }
  return c;
}

이 알고리즘의 시간 복잡도는 두 정수의 길이가 모두 n이라고 할 때 n번 실행되는 for문이 두 번 겹쳐 있기 때문에(0으로 채우는 반복문 제외) O(n²)이다. 이제 카라츠바의 빠른 곱셈 알고리즘에 대해 알아보자. 우선, 두 수를 각각 절반으로 쪼갠다. a와 b가 각각 256자리 수라면, a₁과 b₁은 첫 128자리, a₀과 b₀은 그 다음 128자리를 저장하도록 하는 것이다. 그러면 a와 b를 다음과 같이 나타낼 수 있다.

\(a = a_1 \cdot 10^{128} + a_0\) \(b = b_1 \cdot 10^{128} + b_0\)

카라츠바는 이때 \(a \cdot b\)를 네 개의 조각을 이용해 표현하는 방법을 살펴보았다. 예를 들면, 아래와 같이 표현할 수 있다. \(a \cdot b = (a_1 \cdot 10^{128} + a_0) \cdot (b_1 \cdot 10^{128} + b_0)\) \(= a_1 \cdot b_1 \cdot 10^{256} + (a_1 \cdot b_0 + a_0 \cdot b_1) \cdot 10^{128} + a_0 \cdot b_0\)

이 방법에서는 큰 정수 두 개를 한 번 곱하는 대신, 절반 크기로 나눈 작은 조각을 네 번 곱한다. (10의 거듭제곱과 곱하는 것은 그냥 뒤에 0을 붙이는 시프트 연산으로 구현하면 되니 곱셈으로 치지 않는다.) 이대로도 각각을 재귀 호출해서 해결하면 분할 정복 알고리즘이라고 할 수 있다. 이 방법에서 길이 n인 두 정수를 곱하는데 드는 시간은 덧셈과 시프트 연산에 걸리는 시간 O(n)과 n/2 길이 조각들의 곱셈 네번으로 나눌 수 있다. 하지만, 이 방법의 전체 수행 시간이 O(n²)이 된다는 사실을 증명할 수 있다. 때문에 분할 정복을 구현한 의미가 없어진다.

카라츠바가 발견한 것은 다음과 같이 \(a \cdot b\)를 포현했을 때 네 번 대신 세 번의 곱셈만으로만 이 값을 계산할 수 있다는 점이다.

\[a \cdot b = a_1 \cdot b_1 \cdot 10^{256} + (a_1 \cdot b_0 + a_0 \cdot b_1) \cdot 10^{256} + a_0 \cdot b_0\]

각각의 부분을 아래와 같이 \(z_2\), \(z_1\), \(z_0\)이라고 쓴다. 우선 \(z_0\)와 \(z_2\)를 각각 한 번의 곱셈으로 구한다. 그리고 다음 식을 이용한다. \((a_0+a_1) \cdot (b_0) + (b_1) =\)

\[z_2 : a_0 \cdot b_0\] \[z_1 : a_1 \cdot b_0 + a_0 \cdot b_1\] \[z_0 : a_1 \cdot b_1\] \[= z_2 + z_1 + z_0\]

따라서 위 식의 결과에서 z₀과 z₂를 z₁을 구할 수 있다. 다음과 같은 코드 조각을 이용하면 된다.

z2 = a1 x b1;
z0 = a0 x b0;
z1 = (a0 + a1) x (b0 + b1) - z0 - z2;

이 과정은 곱셈을 세 번밖에 쓰지 않는다. 그러나 나면 이 세 결과를 다시 적절히 조합해 원래 두 수의 답을 구해낼 수 있다. 아래는 이와 같이 구현한 카라츠바 알고리즘의 구현을 작성한 코드이다.

//카라츠바의 빠른 점수 곱셈 알고리즘

//a += b*(10^k);를 구현한다.
void addTo(List<Integer> a, final List<Integer> b, int k);
// a -= 1x를 구현한다. a >= b를 가정한다.
void subForm(List<Integer> a, final List<Integer> b);
//두 긴 정수의 곱을 반환한다.
List<Integer> karatsuba(final List<Integer> a, final List<Integer> b){
  int an = a.size(), bn = b.size();
  //a가 b보다 짧은 경우 둘을 바꾼다.
  if(an < bn) return karatsuba(b, a);
  //기저 사례: a나 b가 비어 있는 경우
  if(an == 0 || bn == 0) return new ArrayList<Integer>();
  //기저 사례: a가 비교적 짧은 경우 O(n^2) 곱셈으로 변경한다.
  if(an <= 50) return multiply(a, b);
  int half = an / 2;
  //a와 b를 밑에서 half 자리와 나머지로 분리한다.
  List<Integer> a0 = new ArrayList<>();
  a0.add(a.get(0), a.get(0) + half);
  List<Integer> a1 = new ArrayList<>();
  a1.add(a.get(0) + half, a.get(a.size()-1));
  List<Integer> b0 = new ArrayList<>();
  b0.add(b.get(0), b.get(0) + Math.min(b.size(), half));
  List<Integer> b1 = new ArrayList<>();
  b1.add(b.get(0) + Math.min(b.size(), half), b.get(b.szie()-1));
  //z2 = a1 * b1
  List<Integer> z2 = karatsuba(a1, b1);
  //z() = a() * b()
  List<Integer> z0 = karatsuba(a0, b0);
  //a() = a() + a1 = b0 + b1
  addTo(a0, a1, 0);
  addTo(b0, b1, 0);
  //z1 = (a() * b()) - z0 - z2;
  List<Integer> z1 = karatsuba(a0, b0);
  subForm(z1, z0);
  subForm(z1, z2);
  //ret = z() + z1 * 10^half + z2 * 10^(half*2)
  List<Integer> ret;
  addTo(ret, z0, 0);
  addTo(ret, z1, half);
  addTo(ret, z2, half + half);
  return ret;
}

카라츠바 알고리즘은 분할한 부분 문제의 답에서 원래 문제의 답을 병합해내는 부분을 개선함으로써 알고리즘의 성능을 향상시킨 좋은 예이다. (어렵지만 아주 잘 알아두도록 해야겠다.) 스트라센(Strassen)의 행렬 곱셈 알고리즘 또한 이와 비슷한 기법을 사용한다.

시간 복잡도 분석.

카라츠바 알고리즘은 두 개의 입력을 절반씩으로 쪼갠 뒤, 세 번 재귀 호출을 하기 때문에 재귀 호출을 한 번이나 두 번만 하던 지금까지의 예제와는 다르게 시간 복잡도를 따로 분석해야 한다. 위 코드에서 병합 단계의 수행 시간은 addTo와 subForm의 수행 시간에 지배되고, 기저 사례의 처리 시간은 multiply의 수행 시간에 지배되는 것을 알 수 있다.

우선 카라츠바 알고리즘의 수행 시간을 병합 단계와 기저 사례의 두 부분으로 나눈다.

먼저 기저 사례를 처리하는 데 드는 총 시간을 알아보면, 위 코드에서 더 긴 숫자의 길이가 50자리보다 짧아지면 multiply를 이용해 답을 계산하기로 했지만, 여기서는 편의를 위해 한 자리 숫자에 도달해야만 multiply를 사옹한다고 가정한다. 자릿수 n이 2의 거듭제곱 \(2^k\)라고 했을 때 재귀 호출의 깊이는 k가 된다. 한 번 쪼갤 때마다 해야 할 곱셈의 수가 세 배씩 늘어나기 때문에 마지막 단계에는 \(3^k\)개의 부분 문제가 있는데, 마지막 단계에서는 두 수 모두 한 자리니까 곱 셈 한 번이면 충분하다.

따라서 곱셈의 수는 O(\(3^k\))가 된다. \(n = 2^k\)라고 가정햇으니 k = lgn이고, 이때 곱셈의 수를 n에 대해 표현하면 아래와 같은 식이 성립된다. O(\(3^k\)) = (\(3^{lgn}\)) = O(\(n^{lg3}\))

lg3 = 1.585이기 때문에 카라츠바 알고리즘이 O(\(n^2\))보다 훨씬 적은 곱셈을 필요로 하는 것을 알 수 있다. 만약 n이 10만이라고 하면 곱셈의 수는 대략 100배!! 정도 차이가 난다.

다음으로 병합 단계에 드는 시간의 총 합을 구하면, addTo와 subForm은 숫자의 길이에 비례하는 시간만이 걸리도록 구현할 수 있다. 따라서 각 단계에 해당하는 숫자의 길이를 모두 더하면 병합 단계에 드는 시간을 계산할 수 있다. 단계가 내려갈 때마다 숫자의 길이는 절반으로 줄고 부분 문제의 개수는 세 배 늘기 때문에, i번째 단계엣 필요한 연산 수는 \(({3 \over 2})^i \cdot n\)이 된다. 따라서 모든 단계에서 필요한 전체 연산의 수는 다음 식에 비례한다. \(n \cdot \sum_{i=0}^{lgn} k({3 \over 2})^i\)

이 함수는 \(n^{lg3}\)과 같은 속도로 증가한다. 따라서 카라츠바 알고리즘의 시간 복잡도는 곱셈이 지배하며, 최종 시간 복잡도는 O(\(n^{lg3}\))이 된다. 단, 카라츠바 알고리즘의 구현은 단순한 O(\(n^{2}\)) 알고리즘보다 훨씬 복잡하기 때문에, 입력의 크기가 작을 경우 O(\(n^{2}\))의 알고리즘보다 느린 경우가 많다는 데 유의해야 한다. 위 코드의 입력된 숫자가 짧을 경우 O(\(n^{2}\)) 알고리즘을 사용하는 것도 이런 이유에서이다.

간단하게? 분할 정복 알고리즘 패러다임에 대해서 알아보았다. 역시 알고리즘은 수학이 필수라는 것을 새삼 다시 느낀다. 요즘 R과 더불어 통계학을 짬을 내서 공부하며 수학의 엄청난 힘을 느끼고 있던터라, 더욱 그런 것 같다. ~~갑자기?~~

다음 알고리즘 포스팅부턴 본격적으로 분할 정복 알고리즘에 대해 알아보는 걸로~

오타나 잘못된 부분을 지적해주시면 감사히 생각하고 수정토록 하겠습니다 :)
참고문헌
구종만, 알고리즘 문제 해결 전략. pp.175~pp.188.