소풍 문제
by Seongjae Moon
블로그를 시작한지도 어느덧 두 달이 되었다. 하루 1 커밋이 목표였지만, 내용의 부실함을 느끼고 주말까지 2 커밋을 목표로 하였는데, 잘 지켜지지 않는다.. 이런 저런 핑계로 공부를 게을리 하는 나 자신을 질책하며, 멈추지 않고 꾸준히 하는 것을 목표로 또 한 주를 마무리 해야겠다.
책에서는 C++를 이용해서 코딩하지만, 스터디를 위해 사용하기로 한 언어가 JAVA이기 때문에 코드는 JAVA로 작성되었으며, 책의 내용을 나름대로 재구성하여 작성하였다.
먼저, 소풍(Picnic) 문제에 대해서 알아보자.
소풍 문제는 그 이름과는 달리 굉장히 슬픈? 문제이다. 아무개 학교에서 아무개 소풍지로 소풍을 가려고 한다. 선생님의 편의상 소풍지에서 두 명씩 짝을 지어 행동을 하게 하려고 한다고 가정하자. 이때, 서로 친하지 않은(두루두루 친하게 지내자.) 친구들이 짝을 이루지 않게 할 수 있는 방법의 수를 구하는 문제이다. 반대로 말하면, 서로 친구인 짝만 만드는 경우의 수를 계산하는 문제이다.
예를 들어보자.
트와이스 학교의 티티반 학생들인 쯔위, 나연, 정연, 사나, 모모, 지효, 채영, 다현, 미나, 성재가 이번에 소풍을 가려고 한다. 티티반은 서로 굉장히 친하지만 그 중에서도 약간 어색한 친구들이 있다고 감히? 가정하자.
티티반을 담당하는 진영 선생님은 서로 어색한 친구들이 짝이 되지 않도록 배려하기 위해서 서로 어색한 친구들이 짝이 되지 않는 경우의 수를 계산하고자 한다고 하자.
책의 내용을 빌리자면, 이러한 “가능한 조합의 수를 계산하는 문제를 푸는 가장 간단한 방법은 완전 탐색을 이용해 조합을 모두 만들어 보는 것이다.” 컴퓨터는 우리가 상상하는 것 이상으로 빠른 연산이 가능하므로, 사람의 힘으론 계산하기 어려운 문제도 빠른 연산 속도로 계산해낼 수 있다.(컴퓨터의 연산 속도를 믿어보자.)
- 문제의 전제 조건은 다음과 같다. 각 학생들의 쌍에 대해 이들이 서로 친구인지 여부가 주어질 때, 학생들을 짝 지을 수 있는 방법의 수를 계산하는 프로그램을 작성한다. 단, 짝이 되는 학생의 일부만 다르더라도 다른 방법으로 본다. 예를 들어, (쯔위, 채영), (성재, 모모), (정연, 미나) < - > (쯔위, 채영), (성재, 다현), (정연, 모모)는 다른 방법이다.
- 시간 및 메로리 제한 프로그램은 1초 내에 실행 되어야 하고, 64MB 이하의 메모리만 사용해야 한다.
- 입력 입력의 첫 줄에는 테스트 케이스의 수 C(C<=50)가 주어진다. 각 테스트 케이스의 첫 줄에는 학생의 수 n(2<=n<=10)와 친구 쌍의 수(0<=m<=n*(n-1)/2)가 주어진다.그 다음 줄에 m개의 정수 쌍으로 서로 친구인 두 학생의 번호가 주어진다. 번호는 모두 0 부터 n-1 사이의 정수이고, 같은 쌍은 입력에 두 번 주어지지 않는다. 단, 학생들의 수는 짝수이다.
- 출력
각 테스트 케이스마다 한 줄에 모든 학생을 친구끼리만 짝지어줄 수 있는 방법의 수를 출력한다.
입력예: 1 2 1 0 1 출력예: 1
문제의 이해.
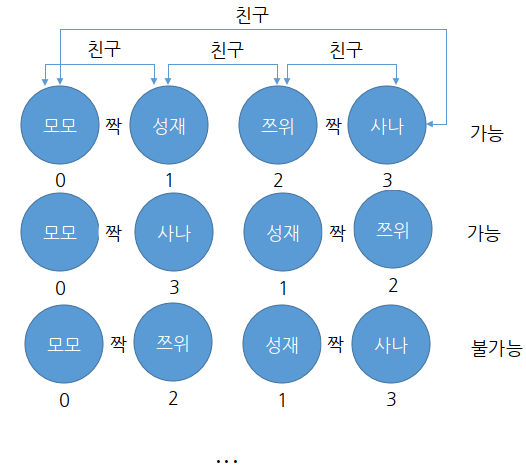 경우의 수를 계산할 때는 항상 특정 형태를 갖는 답만을 세는 것이 중요하다. (중복 제거를 위해) 이를 위해, 같은 답 중에서 사전순으로 가장 먼저 오는 답 하나만을 세는 것이다.
예를 들어, (2,3), (1,0)이나, (1,0), (2,3)은 세지 않지만, (0,1), (2,3)은 세는 것이다. 이 속성을 강제하기 위해서는 각 단계에서 남아 있는 학생들 중 가장 번호가 빠른 학생의 짝을 찾아 주도록 하면 된다. 그렇다면, 소풍 코드를 살펴보자.
경우의 수를 계산할 때는 항상 특정 형태를 갖는 답만을 세는 것이 중요하다. (중복 제거를 위해) 이를 위해, 같은 답 중에서 사전순으로 가장 먼저 오는 답 하나만을 세는 것이다.
예를 들어, (2,3), (1,0)이나, (1,0), (2,3)은 세지 않지만, (0,1), (2,3)은 세는 것이다. 이 속성을 강제하기 위해서는 각 단계에서 남아 있는 학생들 중 가장 번호가 빠른 학생의 짝을 찾아 주도록 하면 된다. 그렇다면, 소풍 코드를 살펴보자.
package algorithm.picnic;
import java.util.*;
public class Picnic {
//10명의 학생의 짝을 담을 boolean형 2차원 배열 선언
static boolean areFriends[][] = new boolean[10][10];
//전체 학생의 수
static int n;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
//테스트 케이스
System.out.print("테스트 케이스?(C<=50):");
int C = sc.nextInt();
int result[] = new int[C];
//테스트 케이스만큼 반복
for(int i = 0; i < C; ++i) {
//학생의 수 입력
System.out.print("학생의 수?(2=<n<=10):");
n = sc.nextInt();
//서로 친구인 학생의 수 입력
System.out.print("서로 친구인 학생의 수?(0<=m<=1부터 n까지의 총합):");
int m = sc.nextInt();
//10명의 학생을 담을 배열 선언(false로 초기화)
boolean taken[] = new boolean[10];
//서로 친구인 학생의 수만큼 반복
for(int j = 0; j < m; ++j) {
System.out.println("서로 친구인 학생 입력?(0<=m<=n-1:)");
int friends1 = sc.nextInt();
int friends2 = sc.nextInt();
//(모모, 성재), (성재, 모모)는 같은 경우이므로, 둘 다 true로 선언.
areFriends[friends1][friends2] = areFriends[friends2][friends1] = true;
}
//경우의 수 계산하여 결과를 보여줄 배열에 할당한다.
result[i] = countParing(taken);
}
//테스트 케이스 수 만큼 반복
for(int i = 0; i < result.length; ++i) {
//결과 출력
System.out.println("결과 : " + result[i]);
}
sc.close();
}
//taken = i번째 학생이 짝을 이미 찾았으면 true 아니면 false
private static int countParing(boolean taken[]) {
//짝을 찾은 인덱스 계산을 위한 변수 선언
int firstFree = -1;
//학생(n)의 수 만큼 반복
for(int i = 0; i < n; ++i) {
//i번 째 인덱스의 값(친구)이 짝이 지어지지 않았다면
if(!taken[i]) {
//해당 인덱스의 값을 짝을 찾을 변수로 변경
firstFree = i;
//짝을 지을 학생을 찾았으므로 반복 중지
break;
}
}
//기저 사례: 모든 학생이 짝을 찾았으면 한 가지 방법을 찾았으니 종료한다.(경우의 수 하나 찾음!)
if(firstFree == -1) {
return 1;
}
//경우의 수를 더할 변수 선언
int ret = 0;
//해당 학생과 친구인지 확인할 변수 = 짝을 찾을 변수(친구) + 1, 짝을 찾을 변수는 전체 학생의 수 만큼 반복
for(int pairWith = firstFree+1; pairWith < n; ++pairWith) {
//해당 인덱스가 친구와 짝이 지어지지 않았고, 해당 학생과 친구이면
if(!taken[pairWith] && areFriends[firstFree][pairWith]) {
//해당 인덱스는 친구이므로 짝을 지어준다.
taken[firstFree] = taken[pairWith] = true;
//경우의 수를 재귀 호출를 통해 반복해서 구한다.
ret += countParing(taken);
//인덱스가 재귀 호출 과정에서 변하므로 false를 할당한다.(해당 친구의 다음 짝을 계산해야 하므로)
taken[firstFree] = taken[pairWith] = false;
}
}
//계산 결과(경우의 수) 반환
return ret;
}
출력예:
테스트 케이스?(C<=50):2
학생의 수?(2=<n<=10):2
서로 친구인 학생의 수?(0<=m<=1부터 n까지의 총합):1
서로 친구인 학생 입력?(0<=m<=n-1:)
0
1
학생의 수?(2=<n<=10):4
서로 친구인 학생의 수?(0<=m<=1부터 n까지의 총합):6
서로 친구인 학생 입력?(0<=m<=n-1:)
0
1
서로 친구인 학생 입력?(0<=m<=n-1:)
1
2
서로 친구인 학생 입력?(0<=m<=n-1:)
2
3
서로 친구인 학생 입력?(0<=m<=n-1:)
3
0
서로 친구인 학생 입력?(0<=m<=n-1:)
0
2
서로 친구인 학생 입력?(0<=m<=n-1:)
1
3
결과 : 1
결과 : 3
위 코드의 순서를 간단하게 정리하면,
1.해당 학생이 짝을 가진 친구인지 확인.
2.(1번을 만족하는 경우)전체 학생을 비교하며 짝을 순서대로 지어줌.
3.(2번을 만족하는 경우)짝을 지어줄 수 있는 모든 경우의 수(기저 사례가 나올 때 까지)를 계산할 때 까지 2번 반복.
시간 복잡도 분석.
이러한 모든 답을 생성해 가며 답의 수를 세는 재귀 호출 알고리즘은 답의 수에 정비례 하는 시간이 걸린다. 따라서 실제로 프로그램을 짜기 전에 답의 수가 얼마나 될지 예측해 보고 모든 답을 만드는 데 시간이 얼마나 오래 걸릴지를 확인해야 한다.
이 문제에서 가장 많은 답을 가질 수 있는 입력은 열 명의 학생이 모두 서로 친구인 경우라고 할 수 있다. 이때 가장 번호가 빠른 학생이 선택할 수 있는 짝은 아홉 명이고, 그 다음 학생이 선택할 수 있는 짝은 일곱 명이다. 이와 같이 나가면 최종 답의 개수는 9x7x5x4x3x1 = 945가 된다.
이렇게 해서 간단하게 Picnic에 대해 알아보았다. 보글 게임과 마찬가지로 책에선 난이도가 ‘하’로 적혀있는 완전탐색 관련 알고리즘 문제이다. 하..후..
계속해서 다음은 게임판 덮기문제 풀이 및 완전 탐색 관련 알고리즘을 마무리 하는 걸로~
- 오타나 잘못된 부분을 지적 해주시면 감사히 생각하고 수정토록 하겠습니다 :)
- 참고문헌
구종만, 알고리즘 문제 해결 전략. pp.155~pp.159.
Subscribe via RSS
