개임판 덮기 문제
by Seongjae Moon
설 연휴를 맞이하여, 코딩에 손을 잠시 놓고 열심히 먹기만 했다. 이러면 안 되겠다는 걸 직감했을 땐 이미 너무 늦어버렸다.(그래도 잘 먹었으니 후회는 없다.) 오늘도 설 연휴를 맞이하여? 다 갖다 붙힌다 열심히 알고리즘 문제를 풀어보자.
책에서는 C++를 이용해서 코딩하지만, 스터디를 위해 사용하기로 한 언어가 JAVA이기 때문에 코드는 JAVA로 작성되었으며, 책의 내용을 나름대로 재구성하여 작성하였다.
먼저, 게임판 덮기(BoardCover) 문제에 대해서 알아보자.
그 이름과는 다르게 게임판을 덮는다는 간단한 문제가 아니다. 이거 이거.. 일단 HxW 크기의 게임판이 있다고 가정 하자. 게임판은 검은 칸과 흰 칸으로 구성된 격자 모양을 하고 있는데 이 중 모든 흰 칸을 세 칸짜리 L자 모양의 블록으로 덮고 싶다.
이때 블록들은 자유롭게 회전해서 놓을 수 있지만, 서로 겹치거나, 검은 칸을 덮거나, 게임판 밖으로 나가서는 안 된다. 게임판이 주어질 때 이를 덮는 방법의 수를 계산하는 프로그램을 작성하는게 목표다.
예를 들어보자.
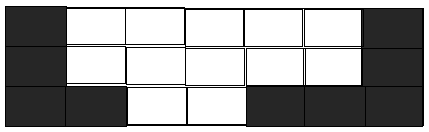 위와 같이 3x7의 총 21개의 칸을 갖는 게임판이 있다고 가정해보자.
위와 같이 3x7의 총 21개의 칸을 갖는 게임판이 있다고 가정해보자.
 위 게임판을 L자 모양으로만 덮는 방법은 위 사진과 같이 2가지 경우의 수가 존재 할 수 있다. 이러한 경우의 수가 총 몇 번 가능한지 세는
위 게임판을 L자 모양으로만 덮는 방법은 위 사진과 같이 2가지 경우의 수가 존재 할 수 있다. 이러한 경우의 수가 총 몇 번 가능한지 세는 어려운 문제라고 할 수 있다. 소풍 문제에서 봤던 것과 같이 재귀 호출을 하기 위해 하트가 그려진 부분을 기준점으로 하여 부분 문제 형식으로 가능한 경우의 수를 계산해 나간다.
- 시간 및 메모리 제한 프로그램은 2초 안에 실행되어야 하며, 64MB 이하의 메모리를 사용해야만 한다.
- 입력 입력의 첫 줄에는 테스트 케이스의 수 C(C<=30)가 주어진다. 각 테스트 케이스의 첫 줄에는 두 개의 정수 H, W(1<=H, W<=20)가 주어진다. 다음 H 줄에 각 W 글자로 게임판의 모양이 주어진다. #은 검은 칸, .는 흰 칸을 나타낸다. 입력에 주어지는 게임판에 있는 흰 칸의 수는 50을 넘지 않는다.
- 출력
각 테스트 케이스마다 한 줄에 하나씩 흰 칸을 모두 덮는 방법의 수를 출력한다.
입력예: 3 3 7 #.....# #.....# ##...## 출력예: 0
문제의 이해.
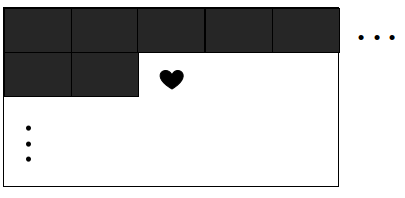 블록을 놓는 순서는 이 문제에서 중요하지 않지만, 같은 모양의 배치를 블록을 놓는 순서에 따라서 여러 번 세면 경우의 수를 중복으로 세개 된다. 따라서 특정한 순서대로 답을 생성하도록 강제할 필요가 있다. 가장 간단한 방법은 재귀 호출의 각 단계마다 아직 빈 칸 중에서 가장 윗 줄, 그 중에서도 가장 왼쪽에 있는칸을 덮도록 하는 것이다. 이렇게 하면 한 답을 한 가지 방법으로밖에 생성할 수 없으므로 중복으로 세는 문제를 해결할 수 있다.
블록을 놓는 순서는 이 문제에서 중요하지 않지만, 같은 모양의 배치를 블록을 놓는 순서에 따라서 여러 번 세면 경우의 수를 중복으로 세개 된다. 따라서 특정한 순서대로 답을 생성하도록 강제할 필요가 있다. 가장 간단한 방법은 재귀 호출의 각 단계마다 아직 빈 칸 중에서 가장 윗 줄, 그 중에서도 가장 왼쪽에 있는칸을 덮도록 하는 것이다. 이렇게 하면 한 답을 한 가지 방법으로밖에 생성할 수 없으므로 중복으로 세는 문제를 해결할 수 있다.
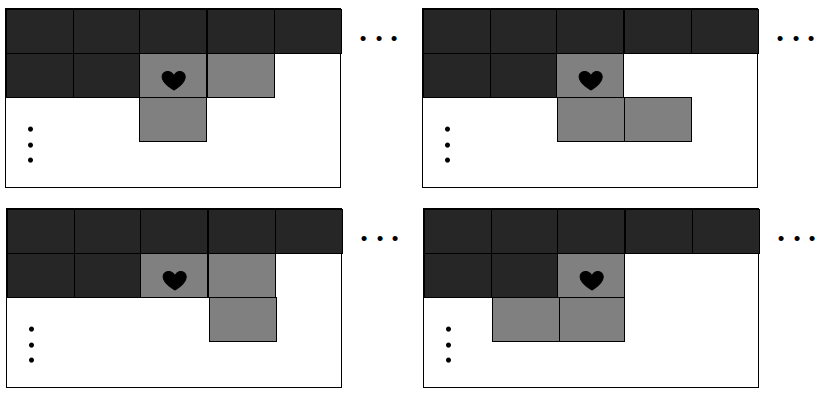
계산을 할 때 항상 빈 칸 중에서 가장 위, 그 중에서도 가장 왼쪽에 있는 칸을 처음 채운다고 가정하기 때문에, 그 왼쪽과 위에 있는 칸은 항상 이미 채워져 있다고 가정할 수 있다. 따라서 각 칸을 채우는 방법은 아래 그림에서 보이는 바와 같이 모두 네가지이다.
재귀 호출 알고리즘은 그림에서 하트로 표시된 첫 번째 빈 칸을 찾은 후 덮을 방법을 하나하나 시도한다. 이 방법이 달라질 때마다 서로 다른 배치가 되므로, 원하는 답은 남은 게임판을 재귀 호출에 넘겨서 얻은 경의의 수를 모둔 더한 수가 된다.
 그렇다면, 게임판 덮기 코드를 살펴보자.
그렇다면, 게임판 덮기 코드를 살펴보자.
package algorithm.boardcover;
import java.util.Scanner;
public class BoardCover {
//주어진 칸을 덮을 수 있는 네 가지 방법
//블록을 구성하는 세 칸의 상대적 위치(dy, dx)의 목록
private static final int coverType[][][] = { { {0, 0}, {1, 0}, {0, 1} },{ {0, 0}, {0, 1}, {1, 1} },{ {0, 0}, {1, 0}, {1, 1} },{ {0, 0}, {1, 0}, {1, -1} }
};
/*
(0,-1) (0,0) (0,1)
(1,-1) (1,0) (1,1)
*/
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
//테스트 케이스.
System.out.print("테스트 케이스?(C<=30):");
int C = sc.nextInt();
//결과를 반환할 배열 선언.
int result[] = new int[C];
//board 선언.
int board[][];
//테스트 케이스만큼 반복.
for(int i = 0; i < C; ++i) {
//세로축 입력(행).
System.out.print("H(1<=H):");
int H = sc.nextInt();
//가로축 입력(열).
System.out.print("W(W<=20):");
int W = sc.nextInt();
//입력받은 보드판 크기 할당.
board = new int[H][W];
for(int j = 0; j < H; ++j) {
System.out.print("#은 검은 칸, .는 흰 칸:");
String cover = sc.next();
for(int k = 0; k < W; ++k) {
//board[i][j] = 1 검은 칸, board[i][j] = 0 아직 덮이지 않은 칸.
board[j][k] = (cover.charAt(k) == '#') ? 1: 0;
}
}
//경의수 구함.
result[i] = cover(board);
}
//테스트 케이스 수만큼 반복.
for(int i = 0; i < result.length; ++i) {
//결과 출력.
System.out.println("결과 : " + result[i]);
}
sc.close();
}
//board의 (y, x)를 type번 방법으로 덮거나, 덮었던 블록을 없앤다.
//delta = 1이면 덮고, -1이면 덮었던 블록을 없앤다.
//만약 블록이 제대로 덮이지 않은 경우 (게임판 밖으로 나가거나, 겹치거나, 같은 칸을 덮을 때) false를 반환한다.
private static boolean set(int[][] board, int y, int x, int type, int delta) {
boolean ok = true;
//L자를 만들 수 있는 형태만큼 반복
for(int i = 0; i < 3; ++i) {
//y의 변화량 = 해당 칸의 y인덱스 + y의 변화 타입.
final int ny = y + coverType[type][i][0];
//x의 변화량 = 해당 칸의 x인덱스 + x의 변화 타입.
final int nx = x + coverType[type][i][1];
//게임판 밖으로 나가거나, 겹치면, false를 반환한다.
if(ny < 0 || ny >= board.length || nx < 0 || nx >= board[0].length) {
ok = false;
//delta가 -1이면 값은 항상 1이 나오므로, false를 반환한다.
}else if((board[ny][nx] += delta) > 1) {
ok = false;
}
}
return ok;
}
//board의 모든 빈 칸을 덮을 수 있는 방법의 수를 반환한다.
//board[i][j] = 1 이미 덮인 칸 혹은 검은 칸.
//board[i][j] = 0 아직 덮이지 않은 칸.
private static int cover(int[][] board) {
//아직 채우지 못한 칸 중 가장 윗줄 왼쪽에 있는 칸을 찾는다.
int y = -1, x = -1;
//보드의 크기(행)만큼 반복.
for(int i = 0; i < board.length; ++i) {
//각 행에 해당하는 크기(열)만큼 반복.
for(int j = 0; j < board[i].length; ++j) {
//아직 덮이지 않은 칸이라면.
if(board[i][j] == 0) {
//덮이지 않은 칸의 인덱스를 할당.
y = i;
x = j;
break;
}
}
//가장 윗줄 칸이 아닐 경우 반복 중지.
if(y != -1) break;
}
//기저 사례: 모든 칸을 채웠으면 1을 반환한다.
if(y == -1) return 1;
int ret = 0;
//4가지 타입의 수만큼 반복.
for(int type = 0; type < 4; ++type) {
//만약 board[y][x]를 type 형태로 덮을 수 있으면 재귀 호출한다.
if(set(board, y, x, type, 1)) {
//경우의 수 합산.
ret += cover(board);
}
//덮었던 블록을 치운다.
set(board, y, x, type, -1);
}
//결과값 반환.
return ret;
}
}
테스트 케이스?(C<=30):1
H(1<=H):3
W(W<=20):7
#은 검은 칸, .는 흰 칸:#.....#
#은 검은 칸, .는 흰 칸:#.....#
#은 검은 칸, .는 흰 칸:##..###
결과 : 2
위 코드의 순서를 간단하게 정리하면,
1. coverType은 네 가지 방법에서 새로 채워질 칸들의 상대 좌표(y의 변화량, x의 변화량)의 목록을 저장한다.
2. set()은 해당 위치에 블록을 놓을 수 있는지 여부를 판단한다.
3. 세 칸 중에 한 칸에 표시를 한 뒤 두 번째 칸에 이미 블록이 놓여있다면, 블록을 치우는 것이 아니라 그 자리에 1을 더한다.(두개의 블록이 겹쳐서 놓여진 상태.)
3. 모든 경우를 계산할 때 까지 set()메소드를 통해 delta에 따라 블록을 놓거나 치운다.
4. 블록을 놓을 수 있는 경우의 수를 반환한다.
시간 복잡도 분석.
이 문제의 답은 한 블록을 놓을 때마다 모두 네 가지의 선택지가 있는데, 우리는 최대 [50/3] = 16개의 블록을 놓기 때문에 가능한 답의 상한은 4^16 = 2^32개가 된다. 이것만 봐서는 엄청난 답의 상한으로 인해 도저히 시간 내에 모두 생성할 수 없을 것 같지만, 실제 입력을 손으로 풀어 보면 각 단계에서 우리가 선택할 수 있는 블록 배치가 크게 제한됨을 알 수 있다.
예를 들어, 흰 칸이 6칸 있는 입력이 주어진다면 이론 상으로는 4^2 = 16가지의 방법이 있어야 하는데, 실제로는 잘 해봐야 두 가지 방법으로밖에 배치할 수 없다.
이렇게 해서 간단하게 BoardCover에 대해 알아보았다. 재귀 호출은 코드의 가독성을 높여 줄뿐더러, 반복 연산을 해야할 경우에 유용하게 사용할 수 있다. 하지만, 역시나 머릿 속에서 잘 떠오르지 않을뿐더러, 기저 사례를 만들어내는 과정이 너무나 어렵게 느껴진다. 정녕 이 길은 나의 길이 아닌 것인가..
소풍 문제와 마찬가지로 난이도’하’로 나와있는 알고리즘이었다. 오늘도 나의 부족함을 뼈저리게 느낀다. 역시 알고리즘 문제를 풀면 머리가 아프다.
다음은 계속해서 재귀호출 문제를 더 풀어보는 걸로~
- 오타나 잘못된 부분을 지적해주시면 감사히 생각하고 수정토록 하겠습니다 :)
- 참고문헌
구종만, 알고리즘 문제 해결 전략. pp.159~pp.164.
Subscribe via RSS
